Group Project

1.    Give 3 definitions of tree. For each definition, please state the resources of definition.

A connected graph with no cycles is called a tree. (Discrete Mathematics With Proof By Eric Gossett, 2009)

A tree is a connected undirected graph with no simple circuits. (Kenneth H.Rosen, Discrete mathematics And Its Application,  Sixth edition ) 

A tree if and only if it is connected, but deleting any of its edges results in a disconnected graph.
(L. Lov´asz and K. Vesztergombi, 1999)

A tree is a mathematical structure that can be viewed as either a graph or as a data structure. The two views are equivalent, since a tree data structure contains not only a set of elements, but also connections between elements, giving a tree graph. (Wolfram MathWorld by Eric Weisstein)

2.    Briefly explain, how to determine a tree?

A tree cannot have a simple circuit.

A tree cannot contain multiple edges or loops.

Any tree must be a simple graph.

3.    What is rooted tree? Describe the characteristics of rooted tree. Please state one example of rooted tree.

A rooted tree is a tree in which one vertex has been designated as the root and every edge is directed away from the root.
Eg

4.    Describe the characteristics/ properties of trees.

A tree must be a simple graph.

A tree cannot have a simple circuit.

A tree is a connected acyclic graph, which is no close path.

A tree has no parallel edges and no loops.

A tree is has (n-1) edges, where n is is the number of vertex.

Theorem 1

A tree with n vertices has (n – 1) edges.

Theorem 2

A full m-ary tree with i internal vertices contains n = (mi + 1) vertices.

Theorem 3

A full m-ary tree with

(i) n vertices has i = (n - 1) /m internal vertices and l = [(m - 1) n + 1] /m leaves,

(ii) i internal vertices has n = mi + 1 vertices and l = (m - 1) i + 1 leaves,

(iii) l leaves has n = (ml - 1) / (m - 1) vertices and i = (l -1) / (m - 1) internal vertices.

Theorem 4

There are at most m^h leaves in an m-ary tree of height h.

5.    State 3 applications of tree. Explain how trees are used in modeling.

Applications:

Binary Search Trees

Decision Trees

Prefix Codes

Modeling:

Computer file systems.

Files in computer memory can be organized into directories. A directory can contain both files and subdirectories. The root directory contains the entire file system. Thus, a file system may be represented by a rooted tree, where the root represents the root directory, internal vertices represent subdirectories, and leaves represent ordinary files or empty directories.

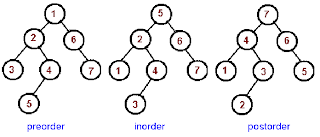
6.    State the definition of Tree Traversal. How many Tree Traversal algorithms exist? Please describe each type of traversal algorithm and state 1 example for each traversal.

Defintion:

Tree Traversal refers to the procedure for systematically visiting every vertex of an ordered rooted tree.

There are 3 Types of Tree Traversal algorithms:

(i)                  Preorder traversal

-Let T be an ordered rooted tree with root r. If T consists only of r, then r is the preorder traversal of T. Otherwise, suppose that T₁,T₂­­­…T_n  are the subtrees at r from left to right in T. The preorder traversal begins by visiting r. It continues by traversing T₁ in preorder, then T₂ in preorder and so on until T_n is traversed in preorder.

(ii)                Inorder traversal

-let T be an ordered rooted tree with root r. If T consists only of r, then r is the inorder traversal of T. Otherwise, suppose that T₁,T₂,…T_n are the subtrees at r from left to right. The inorder traversal begins by traversing T₁ in inorder, then visiting r. It continues by traversing T₂ in inorder, then T₃ in inoorder,… and finally T_n in inorder.

(iii)               Postorder Traversal

-let T be an ordered rooted tree with root r. If T consists only of r, then r is the postorder traversal of T. Otherwise, suppose that T1, T2, … , Tn are the subtrees at r from left to right. The postorder traversal begins by traversing T1 in postorder, then T2 in postorder, … , then Tn in postorder, and ends by visiting r.


Eg)

7.    Briefly explain, what is spanning tree? State 1 application of spanning tree.

A spanning tree of graph is a subgraph of the graph that is a tree containing evert vertex of the graph.

Application of spanning tree: IP multicasting

-       Spanning trees play an important role in multicasting over internet protocol (IP) networks. With IP multicasting, a computer sends a single copy of data over the network and as data reaches intermediate routers, the data are forwarded to one or more other routers so that ultimately all receiving computers in their various sub networks receive these data.

8.    Describe the definition of Minimum Spanning Tree.

A minimum spanning tree in a connected weighted graph is a spanning tree that has the smallest possible sum of weights of its edge

9.    Explain the use of Kruskal’s Algorithm for finding minimum spanning tree and state 1 example applications of Kruskal’s algorithm.

A procedure for producing a minimum spanning tree in a weigthed graph that successively adds edges of least weight that are not already in the tree such that no edge produces a simple circuit when it is added.

                Application of kruskal’s algorithm: Construct road

-A government wants to construct a road network connecting many towns. Suppose each road must connect two towns and be straight. Kruskal's algorithm gives the least expensive tree of roads.

       A Hamiltonian cycle in a dodecahedron. Like all platonic solids, the dodecahedron is Hamiltonian.

Hamilton path    - a simple path in a graph that passes through every vertex exactly once.
Hamilton circuit - a simple circuit in a graph that passes through every vertex exactly once and end back at the 1st vertex.
Dirac's Theorem - if graph is a simple graph with n vertices with n >=3 such that the degree of every vertex in G is at least n / 2, then G has a Hamilton circuit.
Ore's Theorem    - if graph is a simple graph with n vertices with n=> 3 such that deg(u) + deg(v) >= n
for every pair of  nonadjacent vertices U and V in graph, then the graph has a Hamilton circuit
                           (DISCRETE MATHEMATICS AND ITS APPLICATIONS by Kenneth H.Rosen)

                 An Eulerian cycle, also called an Eulerian circuit, Euler circuit, Eulerian tour, or Euler tour
         
                            
An Euler circuit in a graph in a simple circuit containing every edge of Graph.
An Euler Path in Graph is a simple path containing every edge of graph.
Theorem 1 
A connected multigraph with at least two vertices has an Euler if and only if each of its  vertices has even degree.
Theorem 2
A connected multigraph has an Euler path but not an Euler circuit if and only if it has exactly two vertices of odd degree.
                           (DISCRETE MATHEMATICS AND ITS APPLICATIONS by Kenneth H.Rosen)

Server Under Maintainence