Group Project
1.
Give 3 definitions of tree. For each definition, please state
the resources of definition.
A connected graph with no cycles is called a tree. (Discrete Mathematics With Proof By Eric Gossett, 2009)
A tree
is a connected undirected graph with no simple circuits.
(Kenneth H.Rosen, Discrete mathematics And Its Application, Sixth
edition )
A tree if and only if it is
connected, but deleting any of its edges results in a disconnected graph.
(L. Lov´asz and K. Vesztergombi, 1999)
(L. Lov´asz and K. Vesztergombi, 1999)
A tree is a mathematical structure
that can be viewed as either a graph
or as a data structure.
The two views are equivalent, since a tree data structure contains
not only a set of elements, but also connections between elements, giving a
tree graph. (Wolfram MathWorld by Eric Weisstein)
2. Briefly explain, how to
determine a tree?
A tree cannot have a simple circuit.
A tree cannot contain multiple edges
or loops.
Any tree must be a simple graph.
3. What is rooted tree? Describe
the characteristics of rooted tree. Please state one example of rooted tree.
A rooted tree is a tree in which one
vertex has been designated as the root and every edge is directed away from the
root.
Eg
Eg
4. Describe the characteristics/
properties of trees.
A tree must be a simple graph.
A tree cannot have a simple circuit.
A tree is a connected acyclic graph,
which is no close path.
A tree has no parallel edges and no
loops.
A tree is has (n-1) edges, where n is
is the number of vertex.
Theorem 1
A tree with n vertices has (n – 1) edges.
Theorem 2
A full m-ary tree with i internal vertices contains n = (mi + 1)
vertices.
Theorem 3
A full m-ary tree with
(i) n vertices has i = (n - 1) /m internal vertices and l = [(m
- 1) n + 1] /m leaves,
(ii) i internal vertices has n = mi + 1 vertices and l = (m - 1)
i + 1 leaves,
(iii) l leaves has n = (ml - 1) / (m - 1) vertices and i = (l
-1) / (m - 1) internal vertices.
Theorem 4
There are at most mh leaves in an m-ary tree of
height h.
5.
State 3 applications of tree. Explain how trees are used in
modeling.
Applications:
Binary
Search Trees
Decision
Trees
Prefix
Codes
Modeling:
Computer
file systems.
Files in computer
memory can be organized into directories. A directory can contain both files
and subdirectories. The root directory contains the entire file system. Thus, a
file system may be represented by a rooted tree, where the root represents the
root directory, internal vertices represent subdirectories, and leaves
represent ordinary files or empty directories.
6.
State the definition of Tree Traversal. How many Tree
Traversal algorithms exist? Please describe each type of traversal algorithm
and state 1 example for each traversal.
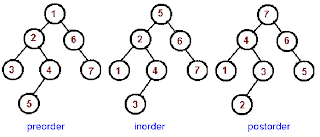
Defintion:
Tree Traversal refers to the procedure for systematically visiting every
vertex of an ordered rooted tree.
There
are 3 Types of Tree Traversal algorithms:
(i)
Preorder
traversal
-Let T be an ordered rooted tree
with root r. If T consists only of r, then r is the preorder traversal of T.
Otherwise, suppose that T1,T2…Tn are the subtrees at r from left to
right in T. The preorder traversal begins by visiting r. It continues by
traversing T1 in preorder, then T2 in preorder and so on
until Tn is traversed in preorder.
(ii)
Inorder
traversal
-let T be an ordered rooted tree
with root r. If T consists only of r, then r is the inorder traversal of T.
Otherwise, suppose that T1,T2,…Tn are the
subtrees at r from left to right. The inorder traversal begins by traversing T1
in inorder, then visiting r. It continues by traversing T2 in
inorder, then T3 in inoorder,… and finally Tn in inorder.
(iii)
Postorder
Traversal
-let T be an ordered rooted tree
with root r. If T consists only of r, then r is the postorder traversal of T.
Otherwise, suppose that T1, T2, … , Tn are the subtrees at r from left to
right. The postorder traversal begins by traversing T1 in postorder, then T2 in
postorder, … , then Tn in postorder, and ends by visiting r.
Eg)
Eg)
7.
Briefly explain, what is spanning tree? State 1 application
of spanning tree.
A spanning tree of graph is a subgraph of the
graph that is a tree containing evert vertex of the graph.
Application of spanning tree: IP multicasting
- Spanning trees play an important role in multicasting over internet
protocol (IP) networks. With IP multicasting, a computer sends a single copy of
data over the network and as data reaches intermediate routers, the data are
forwarded to one or more other routers so that ultimately all receiving
computers in their various sub networks receive these data.
8.
Describe the definition of Minimum Spanning Tree.
A minimum
spanning tree in a connected weighted graph is a spanning tree that has the
smallest possible sum of weights of its edge
9.
Explain the use of Kruskal’s Algorithm for finding minimum
spanning tree and state 1 example applications of Kruskal’s algorithm.
A procedure for
producing a minimum spanning tree in a weigthed graph that successively adds
edges of least weight that are not already in the tree such that no edge
produces a simple circuit when it is added.
Application
of kruskal’s algorithm: Construct road
-A government wants to construct a road
network connecting many towns. Suppose each road must connect two towns and be
straight. Kruskal's algorithm gives the least expensive tree of roads.